Digital video compression/decompression algorithms (codecs) are at the heart of many modern video products, from DVD players to multimedia jukeboxes to video-capable cell phones. Understanding the operation of video compression algorithms is essential for developers of the systems, processors, and tools that target video applications. In this article, we explain the operation and characteristics of video codecs and the demands codecs make on processors. We also explain how codecs differ from one another and the significance of these differences.
Starting with stills
Because video clips are made up of sequences of individual images, or “frames,” video compression algorithms share many concepts and techniques with still-image compression algorithms. Therefore, we begin our exploration of video compression by discussing the inner workings of transform-based still image compression algorithms such as JPEG, which are illustrated in Figure 1.
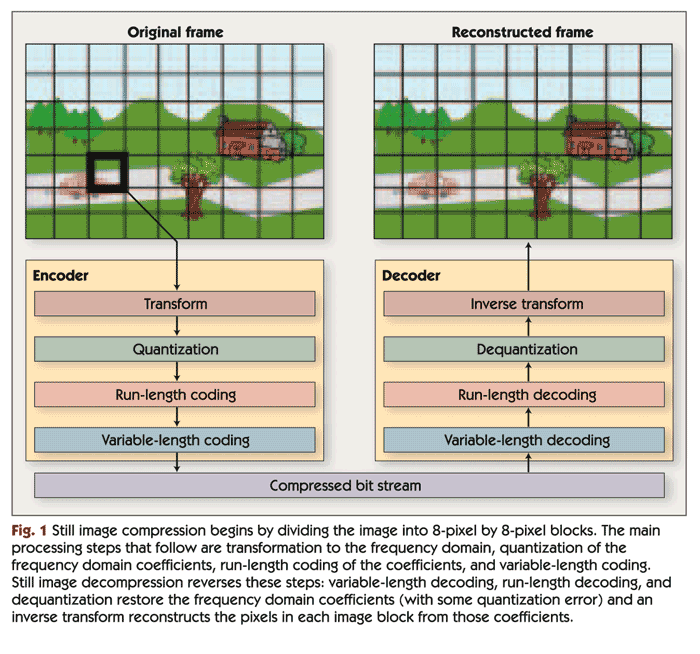
The image compression techniques used in JPEG and in most video compression algorithms are “lossy.” That is, the original uncompressed image can't be perfectly reconstructed from the compressed data, so some information from the original image is lost. The goal of using lossy compression is to minimize the number of bits that are consumed by the image while making sure that the differences between the original (uncompressed) image and the reconstructed image are not perceptible—or at least not objectionable—to the human eye.
Switching to frequency
The first step in JPEG and similar image compression algorithms is to divide the image into small blocks and transform each block into a frequency-domain representation. Typically, this step uses a discrete cosine transform (DCT) on blocks that are eight pixels wide by eight pixels high. Thus, the DCT operates on 64 input pixels and yields 64 frequency-domain coefficients, as shown in Figure 2. (Transforms other than DCT and block sizes other than eight by eight pixels are used in some algorithms. For simplicity, we discuss only the 8x8 DCT in this article.)
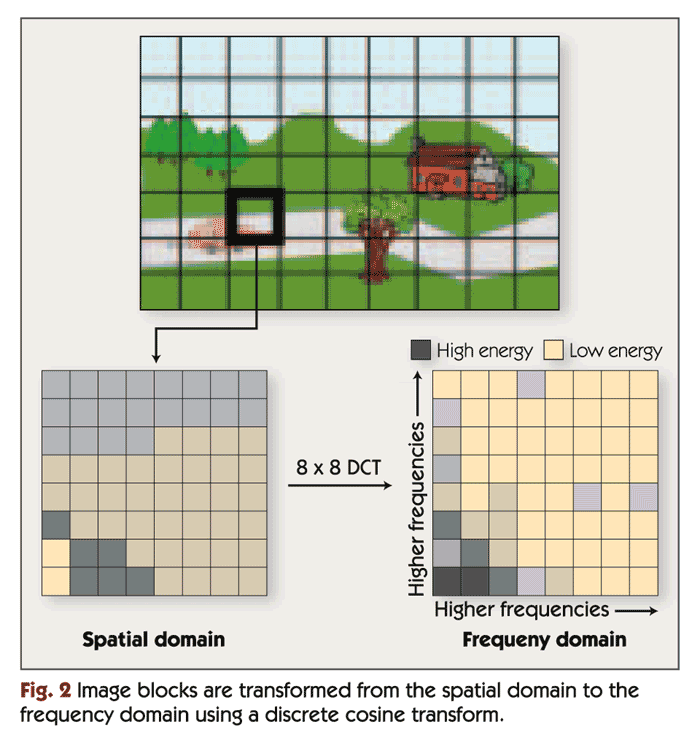
The DCT itself is not lossy; that is, an inverse DCT (IDCT) could be used to perfectly reconstruct the original 64 pixels from the DCT coefficients. The transform is used to facilitate frequency-based compression techniques. The human eye is more sensitive to the information contained in low frequencies (corresponding to large features in the image) than to the information contained in high frequencies (corresponding to small features). Therefore, the DCT helps separate the more perceptually significant information from less perceptually significant information. After the DCT, the compression algorithm encodes the low-frequency DCT coefficients with high precision, but uses fewer bits to encode the high-frequency coefficients. In the decoding algorithm, an IDCT transforms the imperfectly coded coefficients back into an 8x8 block of pixels.
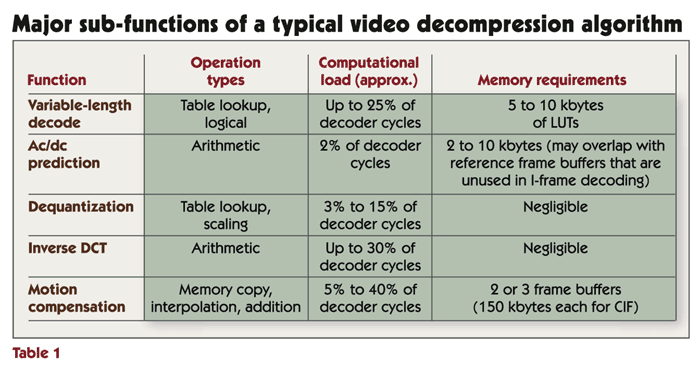
A single two-dimensional eight-by-eight DCT or IDCT requires a few hundred instruction cycles on a typical DSP such as the Texas Instruments TMS320C55x. However, video compression algorithms typically perform a vast number of DCTs and/or IDCTs per second. For example, an MPEG-4 video decoder operating at CIF (352x288) resolution and a frame rate of 30 frames per second (fps) may need to perform as many as 71,280 IDCTs per second, depending on the video content. Combined, these iterations of the IDCT function would require over 40 MHz on a TMS320C55x (without using the DCT accelerator found on many TMS320C55x family chips). In fact, IDCT computation can consume as many as 30 percent of the processor cycles spent in a video decoder implementation.
Because the DCT and IDCT operate on small image blocks, the memory requirements of these functions are typically negligible compared to the size of frame buffers and other data in image and video compression applications.The high computational demand and small memory footprint of the DCT and IDCT functions make them ideal candidates for implementation using dedicated hardware coprocessors.
Choosing the bits: quantization and coding
After the block transform, the DCT coefficients for each 8x8 block are compressed using quantization and coding. Quantization reduces the precision of the DCT coefficients in a biased manner: more bits are used for low-frequency DCT coefficients and fewer bits for high-frequency coefficients. This takes advantage of the fact, as noted above, that human vision is more sensitive to low-frequency information, so the high-frequency information can be more approximate. Many bits are discarded in this step. For example, a 12-bit coefficient may be rounded to the nearest of 32 predetermined values. Each of these 32 values can be represented with a five-bit symbol. In the decompression algorithm, the coefficients are "dequantized"; i.e., the five-bit symbol is converted back to the 12-bit predetermined value used in the encoder. As illustrated in Figure 3, the dequantized coefficients are not equal to the original coefficients, but are close enough so that after the IDCT is applied, the resulting image contains few or no visible artifacts.
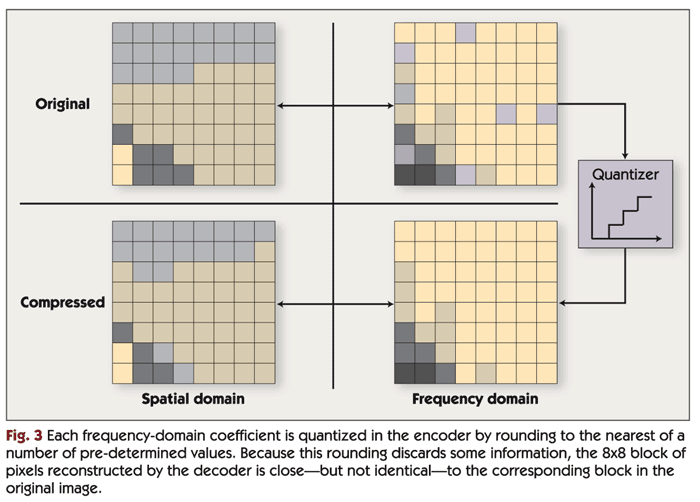
Dequantization can require anywhere from about 3% up to about 15% of the processor cycles spent in a video decoding application. Like the DCT and IDCT, the memory requirements of quantization and dequantization are typically negligible.
Statistically Speaking
Next, the number of bits used to represent the quantized DCT coefficients is reduced by "coding," which takes advantage of some of the statistical properties of the coefficients. After quantization, many of the DCT coefficients—often, the vast majority of the high-frequency coefficients—are zero. A technique called "run-length coding" takes advantage of this fact by grouping consecutive zero-valued coefficients (a &lquo;run&rquo;) and encoding the number of coefficients (the &lquo;length&rquo;) instead of encoding the individual zero-valued coefficients.
Run-length coding is typically followed by variable-length coding (VLC). In variable-length coding, commonly occurring symbols (representing quantized DCT coefficients or runs of zero-valued quantized coefficients) are represented using code words that contain only a few bits, while less common symbols are represented with longer code words. By using fewer bits for the most common symbols, VLC reduces the average number of bits required to encode a symbol thereby reducing the number of bits required to encode the entire image.
On the decompression side, variable-length decoding (VLD) reverses the steps performed by the VLC block in the compression algorithm. Variable-length decoding is much more computationally demanding than variable-length coding. VLC performs one table lookup per symbol (where a symbol is encoded using multiple bits); in contrast, the most straightforward implementation of VLD requires a table lookup and some simple decision making to be applied for each bit. VLD requires an average of about 11 operations per input bit. Thus, the processing requirements of VLD are proportional to the video codec's selected bit rate. VLD can consume as much as 25% of the cycles spent in a video decoder implementation.
In a typical video decompression algorithm, the straightforward VLD implementation described above (which operates on one bit at a time) requires several kilobytes of lookup table memory. It is possible to improve the performance of the VLD by operating on multiple bits at a time, but this optimization requires the use of much larger lookup tables.
Looking at a bigger picture
All of the techniques described so far operate on each 8x8 block independently from any other block. Since images typically contain features that are much larger than an 8x8 block, more efficient compression can be achieved by taking into account the similarities between adjacent blocks in the image.
To take advantage of inter-block similarities, a prediction step is often added prior to quantization of the DCT coefficients. In this step, the encoder attempts to predict the values of some of the DCT coefficients in each block based on the DCT coefficients of the surrounding blocks. The encoder then computes the difference between the actual coefficient and the predicted value and encodes the difference rather than the actual value. At the decoder, the coefficients are reconstructed by performing the same prediction and then adding the difference transmitted by the encoder. Because the difference tends to be small compared to the actual coefficient values, this technique reduces the number of bits required to represent the DCT coefficients.
In predicting the DCT coefficient values of a particular block, the decoder has access only to the DCT coefficients of surrounding blocks that have already been decoded. Therefore, the encoder must predict the DCT coefficients of each block based only on the coefficients of previously encoded surrounding blocks.
JPEG uses a very rudimentary DCT coefficient prediction scheme, in which only the lowest-frequency coefficient (the "DC coefficient") is predicted using simple differential coding. MPEG-4 video uses a more sophisticated scheme that attempts to predict the first DCT coefficient in each row and each column of the 8x8 block. This scheme is referred to as "AC-DC prediction."
AC-DC prediction can require a substantial amount of processing power, and some implementations require large data arrays. However, AC-DC prediction is typically only used a small fraction of the time—when motion compensation (discussed later) is not used—and usually has a negligible impact on average processor load.
Working with color
Color images are typically represented using several "color planes." For example, an RGB color image contains a red color plane, a green color plane, and a blue color plane. When overlaid and mixed, the three planes make up the full color image. To compress a color image, the still-image compression techniques described earlier can be applied to each color plane in turn.
Imaging and video applications often use a color scheme in which the color planes do not correspond to specific colors. Instead, one color plane contains luminance information (the overall brightness of each pixel in the color image) and two more color planes contain color (chrominance) information that when combined with luminance can be used to derive the specific levels of the red, green, and blue components of each image pixel.
Such a color scheme is convenient because the human eye is more sensitive to luminance than to color, so the chrominance planes can often be stored and/or encoded at a lower image resolution than the luminance information. Specifically, video compression algorithms typically encode the chrominance planes with half the horizontal resolution and half the vertical resolution of the luminance plane. Thus, for every 16-pixel by 16-pixel region in the luminance plane, each chrominance plane contains one 8-pixel by 8-pixel block. In typical video compression algorithms, a "macro block" is a 16x16 region in the video frame that contains four 8x8 luminance blocks and the two corresponding 8x8 chrominance blocks.
Adding Motion to the Mix
Video compression algorithms share many of the compression techniques used in still-image compression. A key difference, however, is that video compression can take advantage of the similarities between successive video frames to achieve even better compression ratios. Using the techniques described earlier, still-image compression algorithms such as JPEG can achieve good image quality at a compression ratio of about 10:1. The most advanced still-image codecs may achieve good image quality at compression ratios as high as 30:1. In contrast, video compression algorithms can provide good video quality at ratios of up to 200:1. This increased efficiency is accomplished with the addition of video-specific compression techniques such as motion estimation and motion compensation.
For each macro block in the current frame, motion estimation attempts to find a region in a previously encoded frame (called a "reference frame") that is a close match. The spatial offset between the current block and selected block from the reference frame is called a "motion vector," as shown in Figure 4. The encoder computes the pixel-by-pixel difference between the selected block from the reference frame and the current block and transmits this "prediction error" along with the motion vector. Most video compression standards allow motion-based prediction to be bypassed if the encoder fails to find a good match for the macro block. In this case, the macro block itself is encoded instead of the prediction error.
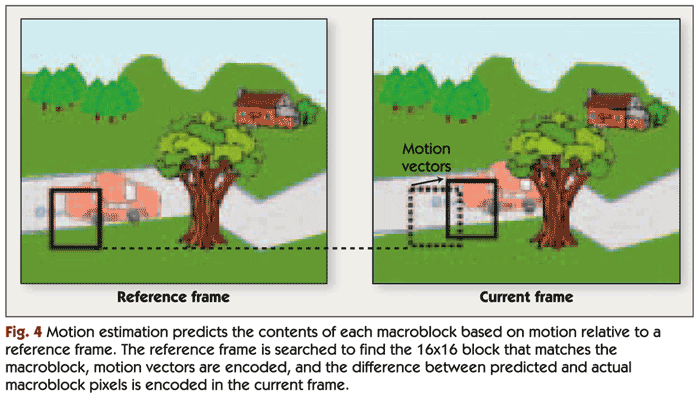
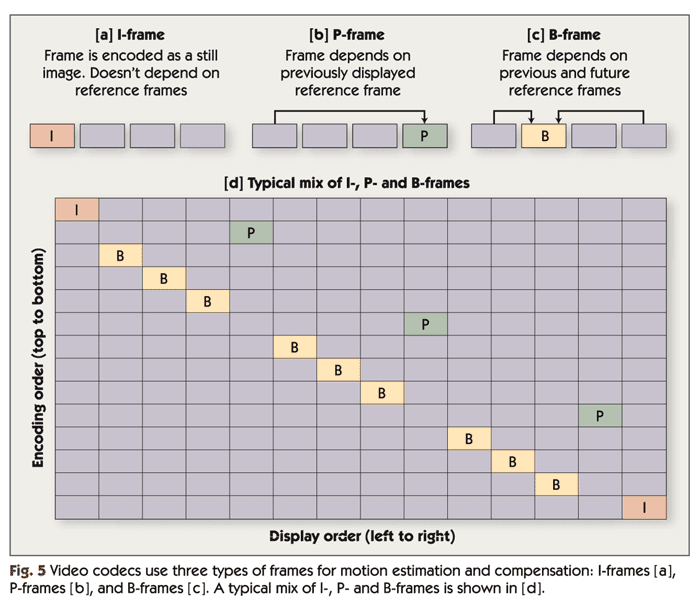
Note that the reference frame isn't always the previously displayed frame in the sequence of video frames. Video compression algorithms commonly encode frames in a different order from the order in which they are displayed. The encoder may skip several frames ahead and encode a future video frame, then skip backward and encode the next frame in the display sequence. This is done so that motion estimation can be performed backward in time, using the encoded future frame as a reference frame. Video compression algorithms also commonly allow the use of two reference frames—one previously displayed frame and one previously encoded future frame.
Video compression algorithms periodically encode one video frame using still-image coding techniques only, without relying on previously encoded frames. These frames are called "intra frames" or "I-frames." If a frame in the compressed bit stream is corrupted by errors, the video decoder can "restart" at the next I-frame, which doesn't require a reference frame for reconstruction.
As shown in Figure 5, frames that are encoded using only a previously displayed reference frame are called "P-frames," and frames that are encoded using both future and previously displayed reference frames are called "B-frames." A typical sequence of frames is illustrated in Figure 5[d].
One factor that complicates motion estimation is that the displacement of an object from the reference frame to the current frame may be a non-integer number of pixels. For example, suppose that an object has moved 22.5 pixels to the right and 17.25 pixels upward. To handle such situations, modern video compression standards allow motion vectors to have non-integer values; motion vector resolutions of one-half or one-quarter of a pixel are common. To support searching for block matches at partial-pixel displacements, the encoder must use interpolation to estimate the reference frame's pixel values at non-integer locations.
The simplest and most thorough way to perform motion estimation is to evaluate every possible 16x16 region in the search area, and select the best match. Typically, a "sum of absolute differences" (SAD) or "sum of squared differences" (SSD) computation is used to determine how closely a candidate 16x16 region matches a macro block. The SAD or SSD is often computed for the luminance plane only, but can also include the chrominance planes. But this approach can be overly demanding on processors: exhaustively searching an area of 48x24 pixels requires over 4.6 billion arithmetic operations per second at CIF (352x288) video resolution and a modest frame rate of 15 frames per second.
Because of this high computational load, practical implementations of motion estimation do not use an exhaustive search. Instead, motion estimation algorithms use various methods to select a limited number of promising candidate motion vectors (roughly 10 to 100 vectors in most cases) and evaluate only the 16x16 regions corresponding to these candidate vectors. One approach is to select the candidate motion vectors in several stages. For example, five initial candidate vectors may be selected and evaluated. The results are used to eliminate unlikely portions of the search area and zero in on the most promising portion of the search area. Five new vectors are selected and the process is repeated. After a few such stages, the best motion vector found so far is selected.
Another approach analyzes the motion vectors previously selected for surrounding macro blocks in the current and previous frames in an effort to predict the motion in the current macro block. A handful of candidate motion vectors are selected based on this analysis, and only these vectors are evaluated.
By selecting a small number of candidate vectors instead of scanning the search area exhaustively, the computational demand of motion estimation can be reduced considerably—sometimes by over two orders of magnitude. But there is a tradeoff between processing load and image quality or compression efficiency: in general, searching a larger number of candidate motion vectors allows the encoder to find a block in the reference frame that better matches each block in the current frame, thus reducing the prediction error. The lower the predication error, the fewer bits that are needed to encode the image. So increasing the number of candidate vectors allows a reduction in compressed bit rate, at the cost of performing more SAD (or SSD) computations. Or, alternatively, increasing the number of candidate vectors while holding the compressed bit rate constant allows the prediction error to be encoded with higher precision, improving image quality.
Even with drastic reductions in the number of candidate motion vectors, motion estimation is the most computationally demanding task in video compression applications. The inclusion of motion estimation makes video encoding much more computationally demanding than decoding. Motion estimation can require as much as 80% of the processor cycles spent in the video encoder. Therefore, many processors targeting multimedia applications provide a specialized instruction to accelerate SAD computations or a dedicated SAD coprocessor to offload this task from the CPU. For example, ARM's ARM11 core provides an instruction to accelerate SAD computation, and some members of Texas Instruments' TMS320C55x family of DSPs provide an SAD coprocessor.
Note that in order to perform motion estimation, the encoder must keep one or two reference frames in memory in addition to the current frame. The required frame buffers are very often larger than the available on-chip memory, requiring additional memory chips in many applications. Keeping reference frames in off-chip memory results in very high external memory bandwidth in the encoder, although large on-chip caches can help reduce the required bandwidth considerably.
Secret Encoders
In addition to the two approaches described above, many other methods for selecting appropriate candidate motion vectors exist, including a wide variety of proprietary solutions. Most video compression standards specify only the format of the compressed video bit stream and the decoding steps and leave the encoding process undefined so that encoders can employ a variety of approaches to motion estimation. The approach to motion estimation is the largest differentiator among video encoder implementations that comply with a common standard. The choice of motion estimation technique significantly affects computational requirements and video quality; therefore, details of the approach to motion estimation in commercially available encoders are often closely guarded trade secrets.
Motion Compensation
In the video decoder, motion compensation uses the motion vectors encoded in the compressed bit stream to predict the pixels in each macro block. If the horizontal and vertical components of the motion vector are both integer values, then the predicted macro block is simply a copy of the 16-pixel by 16-pixel region of the reference frame. If either component of the motion vector has a non-integer value, interpolation is used to estimate the image at non-integer pixel locations. Next, the prediction error is decoded and added to the predicted macro block in order to reconstruct the actual macro block pixels.
Compared to motion estimation, motion compensation is much less computationally demanding. While motion estimation must perform SAD or SSD computation on a number of 16-pixel by 16-pixel regions in an attempt to find the best match for each macro block, motion compensation simply copies or interpolates one such region for each macro block. Still, motion compensation can consume as much as 40% of the processor cycles in a video decoder, though this number varies greatly depending on the content of a video sequence, the video compression standard, and the decoder implementation. For example, the motion compensation workload can comprise as little as 5% of the processor cycles spent in the decoder for a frame that makes little use of interpolation.
Like motion estimation, motion compensation requires the video decoder to keep one or two reference frames in memory, often requiring external memory chips for this purpose. However, motion compensation makes fewer accesses to reference frame buffers than does motion estimation. Therefore, memory bandwidth requirements are less stringent for motion compensation compared to motion estimation, although high memory bandwidth is still desirable for best processor performance.
Polishing the image: deblocking and deringing
Ideally, lossy image and video compression algorithms discard only perceptually insignificant information, so that to the human eye the reconstructed image or video sequence appears identical to the original uncompressed image or video. In practice, however, some artifacts may be visible. This can happen due to a poor encoder implementation, video content that is particularly challenging to encode, or a selected bit rate that is too low for the video sequence, resolution, and frame rate. The latter case is particularly common, since many applications trade off video quality for a reduction in storage and/or bandwidth requirements.
Two types of artifacts, "blocking" and "ringing," are common in video compression applications. Blocking artifacts are due to the fact that compression algorithms divide each frame into 8x8 blocks. Each block is reconstructed with some small errors, and the errors at the edges of a block often contrast with the errors at the edges of neighboring blocks, making block boundaries visible. In contrast, ringing artifacts appear as distortions around the edges of image features. Ringing artifacts are due to the encoder discarding too much information in quantizing the high-frequency DCT coefficients.
Video compression applications often employ filters following decompression to reduce blocking and ringing artifacts. These filtering steps are known as "deblocking" and "deringing," respectively. Both deblocking and deringing use low-pass FIR (finite impulse response) filters to hide these visible artifacts.
Deblocking and deringing filters are fairly computationally demanding. Combined, these filters can easily consume more processor cycles than the video decoder itself. For example, an MPEG-4 simple-profile, level 1 (176x144 pixel, 15 fps) decoder optimized for the ARM9E general-purpose processor core requires that the processor be run at an instruction cycle rate of about 14 MHz when decoding a moderately complex video stream. If deblocking is added, the processor must be run at 33 MHz. If deringing and deblocking are both added, the processor must be run at about 39 MHz—nearly three times the clock rate required for the video decompression algorithm alone.
Post-processing or in-line?
Deblocking and deringing filters can be applied to video frames as a separate post-processing step that is independent of video decompression. This approach provides system designers the flexibility to select the best deblocking and/or deringing filters for their application or to forego these filters entirely in order to reduce computational demands. With this approach, the video decoder uses each unfiltered reconstructed frame as a reference frame for decoding future video frames, and an additional frame buffer is required for the final filtered video output.
Alternatively, deblocking and/or deringing can be integrated into the video decompression algorithm. This approach, sometimes referred to as "loop filtering," uses the filtered reconstructed frame as the reference frame for decoding future video frames. This approach requires the video encoder to perform the same deblocking and/or deringing filtering steps as the decoder in order to keep each reference frame used in encoding identical to that used in decoding. The need to perform filtering in the encoder increases processor performance requirements for encoding, but can improve image quality, especially for very low bit rates. In addition, the extra frame buffer that is required when deblocking and/or deringing are implemented as a separate post-processing step is not needed when deblocking and deringing are integrated into the decompression algorithm. Figure 6 illustrates deblocking and deringing applied "in-loop" or as a post-processing step.
Color Space Conversion
One complication of compressing video streams is that the way color is represented in codecs is different from the way it is represented by video cameras and displays. As noted above, video compression algorithms typically represent color images using luminance and chrominance planes. In contrast, video cameras and displays typically mix red, green, and blue light to represent different colors. Therefore, the red, green, and blue pixels captured by a camera must be converted into luminance and chrominance values for video encoding, and the luminance and chrominance pixels output by the video decoder must be converted to specific levels of red, green, and blue for display. The algorithm for this conversion requires about 12 arithmetic operations per image pixel, not including the interpolation needed to compensate for the fact that the chrominance planes have a lower resolution than the luminance plane at the video compression algorithm's input and output. For a CIF (352x288 pixel) image resolution at 15 frames per second, conversion (without any interpolation) requires over 18 million operations per second. This computational load can be significant; when implemented in software, color conversion requires roughly one-third to two-thirds as many processor cycles as the video decoder.
Know your processing—and your processor
Video compression algorithms employ a variety of signal-processing tasks such as motion estimation, transforms, and variable-length coding. Although most modern video compression algorithms share these basic tasks, there is enormous variation among algorithms and implementation techniques. Table 1 summarizes the key signal-processing tasks in a video decoder and the approximate computational load and memory requirements of each task. As we've discussed, encoder requirements differ from decoder requirements in some important ways, most notably due to the inclusion of the very computationally demanding motion estimation step.


Add new comment